Sayısal modelleme (jeoloji) - Numerical modeling (geology)

Çözmek için süper bilgisayar kullanarak küresel ölçekte sismik dalga yayılımının simülasyonu dalga denklemleri^[1]

İçinde jeoloji, sayısal modelleme jeolojik senaryoların hesaplamalı simülasyonu ile karmaşık jeolojik problemlerin üstesinden gelmek için yaygın olarak uygulanan bir tekniktir.

Sayısal modelleme kullanır Matematiksel modeller jeolojik senaryoların fiziksel koşullarını sayılar ve denklemler kullanarak tanımlamak.^[2] Bununla birlikte, bazı denklemlerinin doğrudan çözülmesi zordur, örneğin kısmi diferansiyel denklemler. Sayısal modellerle jeologlar aşağıdaki gibi yöntemleri kullanabilir: sonlu fark yöntemleri, bu denklemlerin çözümlerine yaklaşmak. Daha sonra bu modellerde sayısal deneyler yapılabilir ve jeolojik süreç bağlamında yorumlanabilecek sonuçlar elde edilebilir.^[2] Bu deneylerle çeşitli jeolojik süreçlerin hem niteliksel hem de niceliksel anlayışı geliştirilebilir.^[3]

Çalışmaya yardımcı olmak için sayısal modelleme kullanılmıştır. kaya mekaniği, kayaların termal geçmişi, tektonik plakaların hareketleri ve Dünya'nın mantosu. Sıvıların akışı sayısal yöntemler kullanılarak simüle edilir ve bu, yeraltı suyu hareket eder veya erimiş dış çekirdeğin hareketlerinin jeomanyetik alanı nasıl verdiğini gösterir.

Tarih

Sayısal modellemenin geliştirilmesinden önce, analog modelleme Doğayı kütle, uzunluk ve zaman açısından azaltılmış ölçeklerle simüle eden, jeolojik sorunları çözmenin en önemli yollarından biriydi,^[4][5] örneğin, oluşumunu modellemek için itme kayışları.^[6] Nispeten basit jeolojik problemleri nicel olarak ele almak için basit analitik veya yarı analitik matematiksel modeller de kullanıldı.^[2]

1960'ların sonlarından 1970'lere kadar, sonlu eleman yöntemleri çözmede süreklilik mekaniği için sorunlar inşaat mühendisliği karmaşık jeolojik olayları modellemek için sayısal yöntemler uyarlandı,^[5][7] Örneğin, katlama^[8][9] ve manto konveksiyonu.^[10] Bilgisayar teknolojisindeki gelişmelerle, sayısal modellerin doğruluğu iyileştirilmiştir.^[2] Sayısal modelleme jeolojik sorunların üstesinden gelmek için önemli bir araç haline geldi,^[2] özellikle Dünya'nın doğrudan gözlemlenmesi zor olan kısımları için örtü ve çekirdek. Yine de analog modelleme, sayısal modellerde yakalanması zor olan jeolojik senaryoların modellenmesinde hala yararlıdır ve analog ve sayısal modellemenin kombinasyonu, Dünya'nın süreçlerinin anlaşılmasını geliştirmek için yararlı olabilir.^[11]

Bileşenler

Sayısal modellemede adımlar. Sayısal modellemenin ilk adımı, gerçek jeolojik senaryoyu nicel olarak yakalamaktır. Örneğin, manto konveksiyon modellemesinde, ısı denklemleri sistemde dolaşan ısı enerjisini tanımlamak için kullanılırken Navier-Stokes denklemleri Viskoz sıvının (manto taşı) akışını tanımlar. İkincisi, bu denklemlerin çözülmesi zor olduğundan, ayrıştırma ve yönetim denklemlerine bir tahmin yapmak için sayısal yöntemler seçilir. Daha sonra bilgisayardaki algoritmalar yaklaşık çözümleri hesaplayabilir. Son olarak, bu çözümlerden yorum yapılabilir. Örneğin, manto konveksiyon modellemesinde, önce mantonun akışı görselleştirilebilir. Daha sonra, akış modelleri ve girdi parametreleri arasındaki ilişki sonuçlandırılabilir.

Genel bir sayısal model çalışması genellikle aşağıdaki bileşenlerden oluşur:^[12][2]

1. Matematiksel model, denklemler ve sınır koşulları gibi jeolojik problemin basitleştirilmiş bir açıklamasıdır.^[2] Modelin bu yönetim denklemleri genellikle kısmi diferansiyel denklemler doğrudan çözmesi zor olan türev of işlevi,^[13] örneğin, dalga denklemi.^[2]
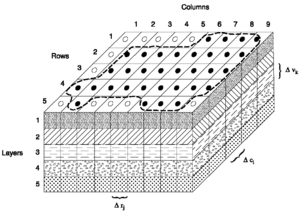
2. Ayrıklaştırma yöntemleri ve sayısal yöntemler, matematiksel modellerdeki bu yönetim denklemlerini ayrık denklemlere dönüştürür.^[2] Bu ayrık denklemler, yönetim denklemlerinin çözümüne yaklaşabilir.^[2] Yaygın yöntemler şunları içerir: sonlu elemanlar, Sonlu fark veya sonlu hacim yöntemi ilgilenilen nesneyi ağ ile daha küçük parçalara (eleman) böler. Bu ayrık denklemler daha sonra her bir elemanda sayısal olarak çözülebilir.^[2] ayrık eleman yöntemi başka bir yaklaşım kullanır, bu yöntem ilgilenilen nesneyi çok sayıda küçük parçacıktan yeniden birleştirir. Basit yönetim denklemleri daha sonra parçacıklar arasındaki etkileşimlere uygulanır.
3. Algoritmalar, çözümü yukarıdaki sayısal yöntemler fikrini kullanarak hesaplayan bilgisayar programlarıdır.^[2]
4. Sayısal modellerin verdiği çözümlerden yorumlar yapılır.^[2]

Özellikleri

İyi bir sayısal model genellikle aşağıdaki özelliklerden bazılarına sahiptir:^[12][2]

• Tutarlı: Sayısal modeller genellikle nesneyi daha küçük öğelere böler. Model tutarlıysa, sayısal modelin sonucu, eleman boyutu neredeyse sıfır olduğunda matematiksel modelin öngördüğü ile hemen hemen aynıdır. Diğer bir deyişle, sayısal modelde kullanılan ayrık denklemler ile matematiksel modeldeki yönetim denklemleri arasındaki hata, ağın alanı (eleman boyutu) sıfıra yaklaştığında sıfıra meyillidir.^[2]
• Kararlı: Kararlı bir sayısal modelde, sayısal yöntemlerin hesaplanması sırasındaki hata artmaz.^[2] Kararsız bir modelin hatası hızla birikecek ve yanlış bir sonuca yol açacaktır. Bir kararlı ve tutarlı Sayısal model, ağın aralığı (öğenin boyutu) son derece küçük olduğunda matematik modeldeki kesin çözümle aynı çıktıya sahiptir.^[2]
• Yakınsama: Sayısal modelin çıktısı, ağ aralığı (eleman boyutu) azaldığında matematiksel modellerdeki geçerli denklemlerin gerçek çözümüne daha yakındır ve bu genellikle sayısal deneyler yapılarak kontrol edilir.^[2]
• Korunmuş: Modellerdeki kütle ve momentum gibi fiziksel büyüklükler korunur.^[2] Matematiksel modellerdeki denklemler genellikle çeşitli koruma kanunlarından türetildiği için, model sonucu bu önermeleri ihlal etmemelidir.^[2]
• Sınırlı: Sayısal model tarafından verilen çözümün matematiksel modellere göre makul fiziksel sınırları vardır, örneğin kütle ve hacim pozitif olmalıdır.^[2]
• Doğru: Sayısal modellerin verdiği çözüm, matematiksel modelin öngördüğü gerçek çözüme yakındır.^[2]

Hesaplama

Aşağıdakiler, jeolojide sayısal modeller geliştirmede fikirlerin bazı temel yönleridir. Öncelikle nesneyi ve hareketi tanımlamanın yolu belirlenmelidir (kinematik açıklama). Ardından, jeolojik sorunları tanımlayan yönetim denklemleri yazılır, örneğin, ısı denklemleri Bir sistemdeki ısı akışını tanımlar. Bu denklemlerden bazıları doğrudan çözülemediğinden, yönetim denklemlerinin çözümüne yaklaşmak için sayısal yöntemler kullanılır.

Kinematik açıklamalar

Sayısal modellerde ve matematiksel modellerde, maddenin hareketini tanımlamak için iki farklı yaklaşım vardır: Euler ve Lagrange.^[14] Jeolojide, her iki yaklaşım da, hesaplama için bir Euler ızgarasının kullanıldığı ve hareketi görselleştirmek için Lagrangian işaretleyicilerin kullanıldığı manto konveksiyonu gibi sıvı akışını modellemek için yaygın olarak kullanılır.^[2] Son zamanlarda, bu iki yaklaşımın avantajlarını birleştirmek için farklı yaklaşımları kullanarak farklı parçaları tanımlamaya çalışan modeller olmuştur. Bu birleşik yaklaşıma, keyfi Lagrange-Euler yaklaşımı.^[15]

Euler

Euler yaklaşımı, kütle ve hız gibi fiziksel niceliklerdeki değişiklikleri dikkate alır. sabit yer zamanla.^[14] Nehir suyunun bir köprüden nasıl geçtiğine bakmaya benzer. Matematiksel olarak, fiziksel büyüklükler konum ve zamanın bir fonksiyonu olarak ifade edilebilir. Bu yaklaşım, doğal sınırı olmayan akışkan ve homojen (tek tip) malzemeler için kullanışlıdır.^[16]

Lagrange

Lagrangian yaklaşımı ise hacim gibi fiziksel büyüklüklerin değişimini dikkate alır. sabit elemanlar zamanla.^[14] Bir nehirde aşağıya doğru akarken belirli bir su molekülü koleksiyonuna bakmaya benzer. Lagrangian yaklaşımını kullanarak, onları çevreden ayırmak için doğal sınırları olan katı nesneleri takip etmek daha kolaydır.^[16]

Yönetim denklemleri

Aşağıda, fiziksel olayları tanımlamak için yaygın olarak kullanılan bazı temel denklemler, örneğin jeolojik bir sistemdeki maddenin nasıl hareket ettiği veya aktığı ve bir sistemde ısı enerjisinin nasıl dağıtıldığı yer almaktadır. Bu denklemler genellikle matematiksel modelin özüdür.

Süreklilik denklemi

Süreklilik denklemi jeolojik nesnenin veya ortamın sürekli olduğunu, yani nesnede boş alan bulunmadığını ifade etmenin matematiksel bir versiyonudur.^[17] Bu denklem genellikle jeolojide sayısal modellemede kullanılır.^[17]

Bir örnek, akışkan kütlesinin süreklilik denklemidir. Yasasına göre kütlenin korunumu, yoğunluğa sahip bir sıvı için ${ displaystyle rho}$ pozisyonda ${ displaystyle x_ {j}}$ sabit bir hacimde ${ displaystyle V}$ sıvının kütle değişim hızı, sınır boyunca dışarıya doğru sıvı akışına eşittir. ${ displaystyle S}$:

${ displaystyle { frac { kısmi} { kısmi t}} int sınırlar _ {V} rho d tau = - int sınırlar _ {S} rho u_ {j} dS_ {j}}$

nerede ${ displaystyle tau}$ hacim öğesi ve ${ displaystyle u_ {j}}$ hızdır ${ displaystyle x_ {j}}$.

Lagrangian biçiminde:^[2]

${ displaystyle { frac {D rho} {Dt}} equiv { frac { kısmi rho} { kısmi t}} + u_ {j} { frac { kısmi rho} { kısmi x_ {j}}} = - rho { frac { kısmi u_ {j}} { kısmi x_ {j}}}}$

Euler formunda:^[2]

${ displaystyle { frac { kısmi rho} { kısmi t}} = { frac { kısmi ( rho u_ {j})} { kısmi x_ {j}}}}$

Bu denklem, mantonun jeolojik zaman ölçekleri üzerinde olması gibi, model sürekli sıvı akışını içerdiğinde yararlıdır.^[2]

Momentum denklemi

Momentum denklemi, uygulanan kuvvete tepki olarak maddenin nasıl hareket ettiğini açıklar. Bir ifadesidir Newton'un ikinci hareket yasası.^[17]

Sabit bir hacim düşünün ${ displaystyle V}$ maddenin. Yasasına göre momentumun korunması, hacim değişim oranı şuna eşittir:^[2]

• dış güç ${ displaystyle F}$ eleman üzerine uygulandı
• artı yüzeye uygulanan normal gerilme ve kayma gerilmesi ${ displaystyle S}$ elemanı sınırlamak
• eksi o yüzeydeki elementin dışına çıkan momentum

${ displaystyle { frac { kısmi} { kısmi t}} int sınırlar _ {V} rho u_ {i} d tau = int sınırlar _ {V} rho F_ {i} d tau + int limits _ {S} sigma _ {ij} dS_ {j} - int limits _ {S} rho u_ {i} u_ {j} dS_ {j}}$

nerede ${ displaystyle tau}$ hacim unsurudur, ${ displaystyle u}$ hızdır.

Basitleştirmeler ve entegrasyonlardan sonra, her hacim için ${ displaystyle V}$, bu denklemin Euler formu şöyledir:^[2][17]

${ displaystyle rho { frac { kısmi u_ {i}} { kısmi t}} + rho u_ {j} { frac { kısmi u_ {i}} { kısmi x_ {j}}} = rho F_ {i} + { frac { kısmi sigma _ {ij}} { kısmi x_ {j}}}}$

Isı denklemi

Isı denklemleri nasıl olduğunu açıklar ısı enerjisi bir sistemde akar.

Enerjinin korunumu yasasından, enerjinin değişim oranı ${ displaystyle E}$ sabit hacimli ${ displaystyle V}$ kütle şuna eşittir:^[2]

• sınırda yapılan iş ${ displaystyle S}$
• artı dış kuvvet tarafından yapılan iş ${ displaystyle F}$ ciltte ${ displaystyle V}$
• eksi ısı iletim sınır ötesi ${ displaystyle S}$
• eksi ısı konveksiyon sınır ötesi ${ displaystyle S}$
• artı dahili olarak üretilen ısı

Matematiksel olarak:

${ displaystyle { frac { kısmi} { kısmi t}} int sınırlar _ {V} rho Ed tau = int sınırlar _ {S} u_ {i} sigma _ {ij} dS_ { j} + int limits _ {V} rho u_ {i} F_ {i} d tau - int limits _ {S} k { frac { kısmi T} { kısmi x_ {j}} } dS_ {j} - int limits _ {S} rho Eu_ {j} dS_ {j} + int limits _ {V} rho Hd tau}$

nerede ${ displaystyle tau}$ hacim unsurudur, ${ displaystyle u}$ hızdır ${ displaystyle T}$ sıcaklık ${ displaystyle k}$ ... iletim katsayısı ve ${ displaystyle H}$ ısı üretim hızıdır.^[2]

Sayısal yöntemler

2B sonlu eleman ağına bir örnek. Alan, çok sayıda üst üste binmeyen üçgene (elemanlar) bölünmüştür. Düğümler köşeler üçgenler.

Sayısal yöntemler, matematiksel modellerde geçerli denklemlere yaklaşma teknikleridir.

Yaygın sayısal yöntemler şunları içerir: sonlu eleman yöntemi, spektral yöntem, sonlu fark yöntemi, ve sonlu hacim yöntemi. Bu yöntemler, yönetim çözümüne yaklaşmak için kullanılır. diferansiyel denklemler alanı ağlara veya ızgaralara ayırarak ve ağdaki tek tek öğelere veya düğümlere daha basit denklemler uygulayarak matematiksel modelde.^[2][18]

Medya oynatın

Sonlu elemanlar yöntemiyle yaklaşık dalga denklemleri. Alan, çok sayıda üçgene bölünmüştür. Ağdaki düğümlerin değerleri, bir dalganın bölgede nasıl yayıldığını göstererek hesaplanır.

ayrık eleman yöntemi başka bir yaklaşım kullanır. Nesne, küçük parçacıklardan oluşan bir topluluk olarak kabul edilir.^[19]

Sonlu eleman yöntemi

sonlu eleman yöntemi nesneyi (veya etki alanını) daha küçük, üst üste binmeyen öğelere (veya alt etki alanlarına) böler ve bu öğeler düğümlere bağlanır. İçin çözüm kısmi diferansiyel denklemler daha sonra daha basit eleman denklemleriyle yaklaştırılır, genellikle polinomlar.^[2][20][21] Daha sonra bu eleman denklemleri, tüm nesne için denklemler halinde birleştirilir, yani her bir elemanın katkısı, tüm nesnenin tepkisini modellemek için toplanır.^[2][20][21] Bu yöntem genellikle mekanik problemleri çözmek için kullanılır.^[21] Aşağıdakiler, sonlu eleman yöntemini kullanmanın genel adımlarıdır:^[21]

1. Öğe türünü seçin ve nesneyi alt bölümlere ayırın. Yaygın eleman türleri üçgen, dörtgen, dört yüzlü vb. içerir.^[21] Farklı problemler için farklı tipte elemanlar seçilmelidir.
2. Yer değiştirme işlevine karar verin. Yer değiştirme işlevi, öğelerin nasıl hareket edeceğini yönetir. Doğrusal, ikinci dereceden veya kübik polinom işlevler yaygın olarak kullanılmaktadır.^[21]
3. Yer değiştirme-şekil değiştirme ilişkisine karar verin. Elemanın yer değiştirmesi, teknik olarak adlandırılan şekilde elemanın şeklini değiştirir veya deforme eder. Gerginlik. Bu ilişki, yer değiştirme nedeniyle elemanın ne kadar gerilme yaşadığını hesaplar.^[21]
4. Gerinim-gerilme ilişkisine karar verin. Elementin deformasyonu indükler stres olan öğeye güç öğeye uygulanır. Bu ilişki, elemanın gerilim nedeniyle yaşadığı gerilme miktarını hesaplar. Bu ilişkinin örneklerinden biri Hook kanunu.^[21]
5. Elemanlar için rijitlik ve rijitlik matrisinin denklemlerini türetin. Stres ayrıca elemanın deforme olmasına neden olur; sertlik Elemanların (sertliği) strese tepki olarak ne kadar deforme olacağını gösterir. Elemanların farklı yönlerdeki sertliği, matris hesaplama sırasında daha basit işlem için form.^[21]
6. Eleman denklemlerini global denklemlerle birleştirin. Her elemanın katkıları, tüm sistemi tanımlayan bir dizi denklemle özetlenir.^[21]
7. Sınır koşullarını uygulayın. Sınırda sıcaklık, stres ve diğer fiziksel büyüklükler gibi önceden tanımlanmış koşullar, sistemin sınırına dahil edilir.^[21]
8. Yer değiştirmeyi çözün. Zaman ilerledikçe, elementlerin yer değiştirmesi adım adım çözülür.^[21]
9. Zorlanma ve stres için çözün. Yer değiştirme hesaplandıktan sonra, şekil değiştirme ve gerilme, 3. ve 4. adımlardaki ilişkiler kullanılarak hesaplanır.^[21]

Çözümü Burger Denklemi, şok dalgalarının nasıl davrandığını açıklayan spektral yöntem. Etki alanı önce dikdörtgen ağa bölünür. Bu yöntemin fikri, sonlu elemanlar yöntemine benzer.

Spektral yöntem

spektral yöntem sonlu eleman yöntemine benzer.^[22][23] En büyük fark, spektral yöntemin kullanmasıdır temel fonksiyonlar, muhtemelen kullanarak Hızlı Fourier Dönüşümü (FFT) bu, işlevi çok sayıda basit işlevin toplamına yaklaştırır.^[22][23] Bu tür temel işlevler daha sonra tüm etki alanına uygulanabilir ve yönetime yaklaşık olarak kısmi diferansiyel denklemler.^[2][22][23] Bu nedenle, her hesaplama tüm alandaki bilgileri hesaba katarken, sonlu elemanlar yöntemi yalnızca komşuluktan bilgileri alır.^[22][23] Sonuç olarak, spektral yöntem üssel olarak yakınsar ve zaman veya uzayda yüksek değişkenlik içeren problemleri çözmek için uygundur.^[22][23]

Sonlu hacim yöntemi

sonlu hacim yöntemi aynı zamanda sonlu eleman yöntemine benzer. Aynı zamanda, ilgilenilen nesneyi daha küçük hacimlere (veya elemanlara) böler, ardından fiziksel nicelikler, bu miktarların farklı yüzler boyunca akışları olarak kontrol hacmi üzerinden çözülür.^[2][24] Kullanılan denklemler genellikle kütle ve enerji gibi fiziksel büyüklüklerin korunmasına veya dengesine dayanır.^[24][25]

Sonlu hacim yöntemi, sonlu elemanlar yöntemi gibi düzensiz ağlara uygulanabilir. Eleman denklemleri hala fiziksel olarak anlamlıdır. Bununla birlikte, eleman denklemlerinin yüksek dereceli versiyonu iyi tanımlanmadığı için daha iyi doğruluk elde etmek zordur.^[2][24][25]

Sonlu fark yöntemi

sonlu fark yöntemi yaklaşık diferansiyel denklemler yaklaşık olarak türev Birlikte fark denklemi çözülmesi gereken en önemli yöntem hangisidir kısmi diferansiyel denklemler.^{[26][27][28][29]}

Sonlu fark yöntemi

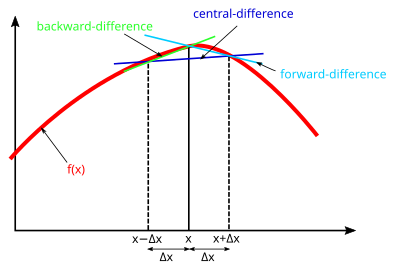
Bir işlevi düşünün ${ displaystyle f (x)}$ sürekli ve sonlu fonksiyonları olan tek değerli türevlerle ${ displaystyle x}$, göre Taylor teoremi:^[30]

${ displaystyle f (x + Delta x) = f (x) + Delta xf '(x) + { frac {1} {2}} Delta x ^ {2} f' '(x) + { frac {1} {6}} Delta x ^ {3} f '' '(x) + cdots}$

ve

${ displaystyle f (x- Delta x) = f (x) - Delta xf '(x) + { frac {1} {2}} Delta x ^ {2} f' '(x) - { frac {1} {6}} Delta x ^ {3} f '' '(x) + cdots}$

Yukarıdaki ifadeleri özetlemek gerekirse:^[30]

${ displaystyle f (x + Delta x) + f (x- Delta x) = 2f (x) + Delta x ^ {2} f '' (x) + { text {4'ün kuvvetinden daha yüksek terimler }} Delta x}$

4. kuvvetten daha yüksek olan terimleri göz ardı edin ${ displaystyle x}$, sonra:^[30]

${ displaystyle f '' (x) simeq { frac {1} { Delta x ^ {2}}} sol [f (x + Delta x) -2f (x) -f (x- Delta x )sağ]}$

${ Displaystyle f '(x) simeq { frac {1} {2 Delta x}} sol [f (x + Delta x) -f (x- Delta x) sağ]}$

Yukarıdakiler merkezi fark türevlerin yaklaştırılması,^[30] bu da yaklaşık olarak ileri fark:

${ Displaystyle f '(x) simeq { frac {1} { Delta x}} sol [f (x + Delta x) -f (x) sağ]}$

veya geriye doğru fark:

${ Displaystyle f '(x) simeq { frac {1} { Delta x}} sol [f (x) -f (x- Delta x) sağ]}$

Sonlu farkların doğruluğu, daha yüksek dereceli terimler kullanıldığında iyileştirilebilir.

Ayrık eleman yöntemi

Ayrık eleman yöntemini kullanan bir model örneği, fotoğrafını kullanan Peter A. Cundall parçacıkları başlatmak için

ayrık eleman yöntemi Bazen ayrı eleman yöntemi olarak adlandırılan, süreksizliklerin özelliklerini açıkça modelleyebildiğinden, genellikle eklemler ve yataklama gibi çatlakları olan kayalar gibi süreksiz malzemeleri modellemek için kullanılır.^[19] Bu yöntem simüle etmek için geliştirilmiştir kaya mekaniği Başlangıçta sorunlar.^[19][31]

Bu yöntemin ana fikri, nesneleri daha küçük parçacıkların bir topluluğu olarak modellemektir.^[19] inşa etmeye benzer kumdan kale. Bu parçacıklar, küre gibi basit geometridir. Her parçacığın hız gibi fiziksel büyüklükleri, aralarındaki temaslarda sürekli olarak güncellenir.^[19] Bu model, büyük miktarda parçacık kullanılması gerektiğinden, hesaplama açısından nispeten yoğundur.^[19] özellikle eğim gibi büyük ölçekli modeller için.^[32] Bu nedenle, bu model genellikle küçük ölçekli nesnelere uygulanır.

Bağlı parçacık modeli

Birbirine yapışan veya birbirine kenetlenen mineral taneciklerinden oluşan kristal kayalar gibi tanecikli malzemelerden oluşmayan nesneler vardır. Parçacıklar arasındaki bu kohezyonu veya simantasyonu modellemek için parçacıklar arasında bir miktar bağ eklenir. Bu tür modele bağlı parçacık modeli de denir.^[33][34][35]

Başvurular

Sayısal modelleme, jeolojinin farklı alanlarındaki problemleri çeşitli ölçeklerde modellemek için kullanılabilir. Jeoloji Mühendisliği, jeofizik, jeomekanik, jeodinamik, kaya mekaniği, ve hidrojeoloji. Aşağıda jeolojide sayısal modelleme uygulamalarının bazı örnekleri verilmiştir.

Örneklerden çıkma ölçeği

Kaya mekaniği

Sayısal modelleme, farklı alanlarda yaygın olarak uygulanmıştır. kaya mekaniği.^[3] Kaya, modellenmesi zor bir malzemedir çünkü kaya genellikle:^[3]

• Süreksiz: Bir kaya kütlesinde çok sayıda kırık ve mikro çatlak vardır.^[36] ve kaya kütlesindeki boşluk hava ve su gibi başka maddelerle dolu olabilir.^[3] Süreksizliklerin kaya kütlesi üzerinde büyük etkileri olduğundan, bu süreksizlikleri tam olarak yakalamak için karmaşık bir modele ihtiyaç vardır.^[3]
• Anizotropik: Kaya kütlesinin özellikleri, örneğin geçirgenlik (sıvının akmasına izin verme yeteneği), farklı yönlerde değişiklik gösterebilir.^[3][36]
• Homojen olmayan: Kaya kütlesinin farklı kısımlarının özellikleri farklı olabilir.^[3][36] Örneğin, fiziksel özellikler kuvars tahıllar ve feldispat tahıllar farklıdır granit.^[37][38]
• Elastik değil: Kaya, stres giderildikten sonra orijinal şekline mükemmel bir şekilde geri dönemez.^[36][3]

Kayanın davranışlarını modellemek için, yukarıdaki tüm özellikleri hesaba katan karmaşık bir modele ihtiyaç vardır.^[3] Kayayı bir süreklilik olarak modelleyen birçok model vardır. Sonlu fark, sonlu elemanlar, ve sınır öğesi yöntemleri. Dezavantajlardan biri, bu modellerde genellikle çatlakları ve diğer süreksizlikleri modelleme yeteneğinin sınırlı olmasıdır.^[39] Kayayı süreksizlik olarak modelleyen modeller, ayrık eleman ve ayrık kırılma ağı yöntemler de yaygın olarak kullanılmaktadır.^[3][35] Her iki yöntemin kombinasyonları da geliştirilmiştir.^[3]

Sayısal modelleme, sayısal deneyler yaparak kayadaki mekanik süreçlerin anlaşılmasını geliştirir ve tasarım ve inşaat işleri için kullanışlıdır.^[3]

Bölgesel ölçek

Termokronoloji

Öngörmek ve açıklamak için sayısal modelleme kullanılmıştır. termal tarih Dünyanın kabuk jeologların termokronolojik verileri yorumlamalarını geliştirmelerine olanak tanıyor.^[40] Termokronoloji, bir kayanın belirli bir sıcaklığın altına düştüğü zamanı gösterebilir.^[41] Fayların gelişmesi ve yüzey erozyonu gibi jeolojik olaylar, yüzeyde toplanan örneklerin termokronolojik modelini değiştirebilir ve bu verilerle jeolojik olayları sınırlandırmak mümkündür.^[41] Modeli tahmin etmek için sayısal modelleme kullanılabilir.

Yerkabuğunun termal modellemesinin zorlukları, esas olarak düzensizliği ve Dünya yüzeyindeki değişiklikleri içerir (esas olarak erozyon ) Zaman boyunca. Bu nedenle, modellemek için morfolojik Dünya yüzeyindeki değişiklikler, modellerin zamanla değişen ve düzensiz ağlara sahip sınır koşullarıyla ısı denklemlerini çözmesi gerekir.^[42]

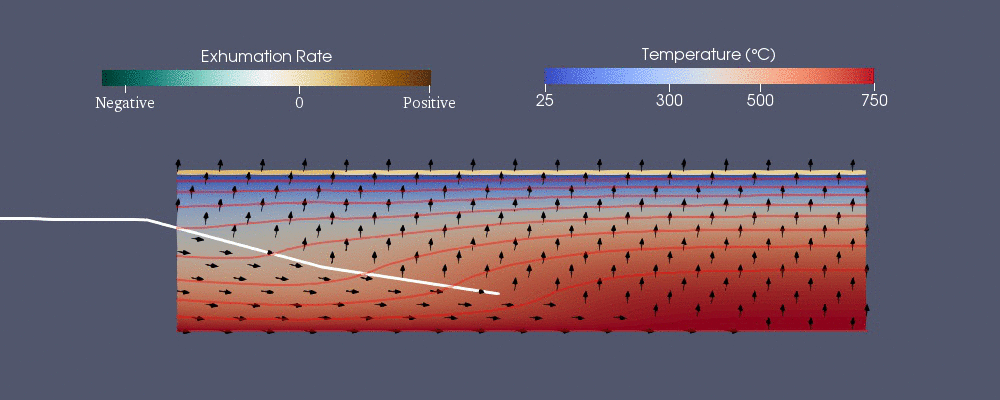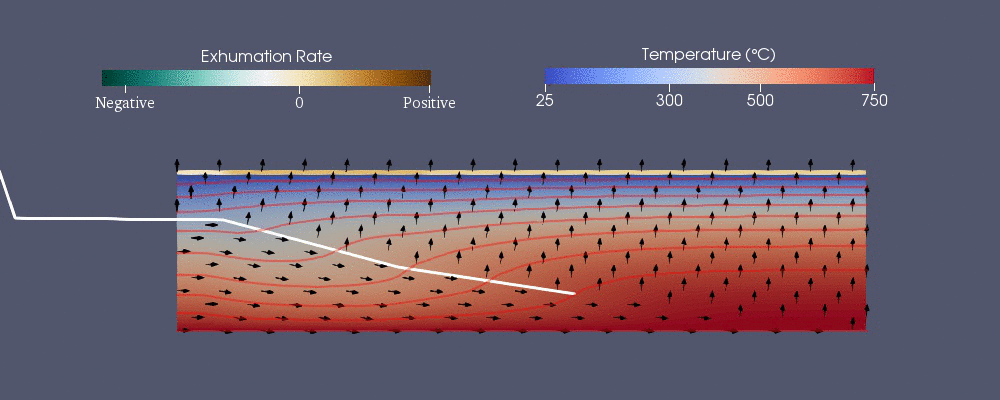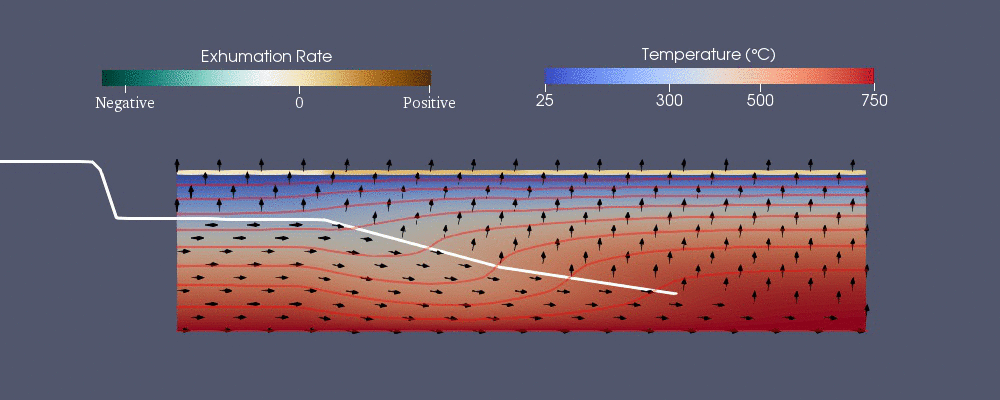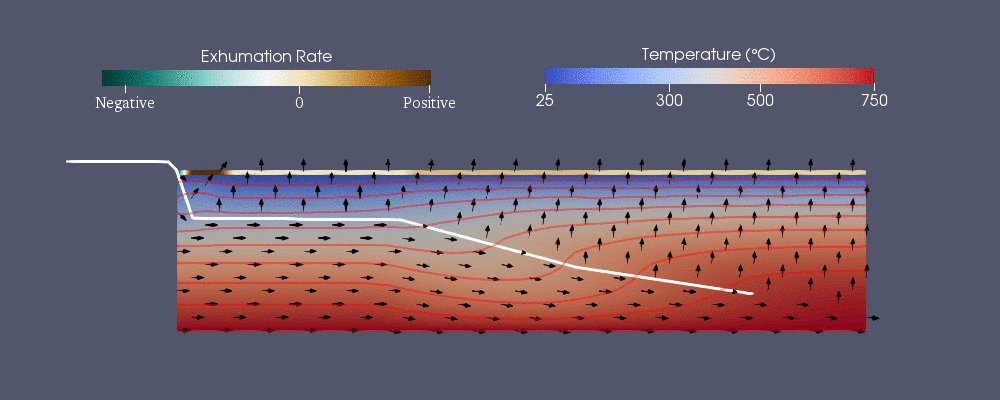
Pecube

Pecube, termokronolojik modeli tahmin etmek için geliştirilen sayısal modellerden biridir.^[42] Aşağıdaki genelleştirilmiş ısı transfer denklemini çözer tavsiye sonlu eleman yöntemini kullanarak.^[40] Sağ taraftaki ilk üç terim, tarafından aktarılan ısıdır. iletim içinde ${ displaystyle x}$, ${ displaystyle y}$ ve ${ displaystyle z}$ yol tarifi ${ displaystyle A}$ tavsiyedir.

$${ displaystyle { frac { kısmi T} { kısmi t}} + u { frac { kısmi T} { kısmi x}} + v { frac { kısmi T} { kısmi y}} + w { frac { kısmi T} { kısmi z}} = { frac { kısmi} { kısmi x}} kappa { frac { kısmi T} { kısmi x}} + { frac { kısmi} { kısmi y}} kappa { frac { kısmi T} { kısmi y}} + { frac { kısmi} { kısmi z}} kappa { frac { kısmi T} { kısmi z}} + A}$$

Termal ve mezardan çıkarma bir hareketin oluşturduğu kabuğun desenleri hata. Simülasyon, Pecube [Helsinki Üniversitesi Geodynamics Group (HUGG) sürümü].^[42][43][44] Model üç boyutludur;^[42][43] şekil basitlik açısından modelin bir dilimini göstermektedir. Şekilde beyaz çizgi, hata. Küçük siyah oklar, malzemenin o noktadaki hareket yönünü gösterir. Kırmızı çizgiler izotermdir (çizginin noktası aynı sıcaklıktadır). Pecube modeli hem Eulerian hem de Lagrangian yaklaşımlarını kullanır.^[42] Fay sabit olarak kabul edilebilir ve kabuk hareketlidir. Başlangıçta kabuğun sıcaklığı derinliğe bağlıdır. Derinlik ne kadar derinse malzeme o kadar sıcaktır. Bu olay sırasında fay boyunca kabuğun hareketi malzemeyi farklı sıcaklıklarda hareket ettirir. Asma duvarda (fayın üstündeki blok), daha derin derinliklerden daha sıcak malzeme yüzeye doğru hareket eder; taban duvarında daha sığ derinlikteki daha soğuk malzeme (fayın altındaki blok) daha derine hareket eder. Malzemenin akışı, kayadaki termokronometreleri sıfırlayabilecek olan kabuğun termal modelini (izoterm, fay boyunca bükülür) değiştirir. Öte yandan, mezardan çıkarma oranı ayrıca kayadaki termokronometreleri de etkiler. Pozitif bir mezar açma oranı, kayanın yüzeye doğru hareket ettiğini gösterirken, negatif bir mezar açma oranı, kayanın aşağı doğru hareket ettiğini gösterir. Fay geometrisi, yüzeydeki desen açma oranını etkiler.

Hidrojeoloji

İçinde hidrojeoloji yeraltı suyu akışı genellikle sonlu elemanlar yöntemi ile sayısal olarak modellenir^[45][46][47] ve sonlu farklar yöntemi.^[48] Mesh yeterince ince ise bu iki yöntemin benzer sonuçlar verdiği gösterilmiştir.^[49][50]

Sonlu fark kullanılan ızgara MODFLOW

MODFLOW

Yeraltı suyu akışının modellenmesinde iyi bilinen programlardan biri, MODFLOW tarafından geliştirilmiştir Amerika Birleşik Devletleri Jeolojik Araştırması. Ücretsizdir ve açık kaynaklı program yeraltı suyu koşullarını modellemek için çerçeve olarak sonlu farklar yöntemini kullanır. İlgili programlardaki son gelişmeler, aşağıdakiler dahil daha fazla özellik sunar:^[51][52]

• Yeraltı suyu ve yüzey suyu sistemleri arasındaki etkileşimler^[51]
• Taşımacılığı çözünenler^[51]
• Tuzlu su gibi değişken yoğunluklu sıvı akışı^[51]
• Akifer sistemlerinin sıkıştırılması^[51]
• Arazi çökmesi^[51]
• Yeraltı suyu yönetimi^[51]

Kabuk dinamiği

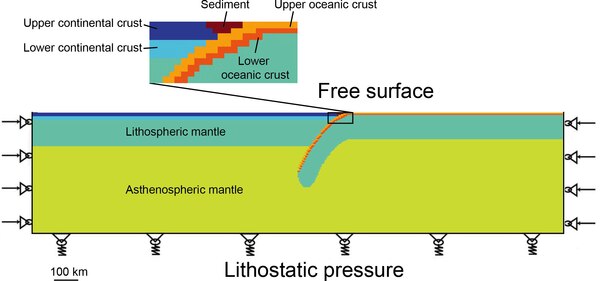
reoloji Kabuk ve litosferin (malzemelerin gerilmeye tepkisi) karmaşıktır, çünkü serbest bir yüzey (kara yüzeyi) ve plastisite ve esneklik Kabuk materyallerinin dikkate alınması gerekir.^[2] Modellerin çoğu, Lagrangian mesh ile sonlu eleman yöntemlerini kullanır.^[2] Bir kullanım, deformasyon ve kinematik çalışmasıdır. yitim.^[53][54]

FLAC

Continua'nın Hızlı Lagrange Analizi (FLAC) kabuk dinamiklerinin modellenmesinde en popüler yaklaşımlardan biridir.^[2] Yaklaşım hızlı denklemlerini çözerken itme ve süreklilik bir matris kullanmadan, dolayısıyla hızlıdır, ancak zaman adımları yeterince küçük olmalıdır.^[55] Yaklaşım 2D olarak kullanılmıştır,^[56][57][58] 2.5D,^[59] ve 3D^[60] 2.5D sonuçlarının, iki boyutlu sonuçların birden çok diliminin birleştirilmesiyle elde edildiği kabuk dinamikleri çalışmaları.^[2]

Bu şekil, tektonik evrim çalışmasında kullanılan sayısal modelin kurulumunu göstermektedir. Cathaysia Bloğu,^[53] güneydoğu kesimini oluşturan Güney Çin kartonu.^[61] Bu model, adı verilen kodu kullanır Flamar, sonlu fark ve sonlu eleman yöntemlerini birleştiren FLAC benzeri bir koddur.^[53] Bu Lagrangian ağda kullanılan eleman dörtgendir.^[53] Arazi yüzeyine uygulanan sınır koşulları serbesttir ve bu erozyon ve tortu birikiminden etkilenir.^[53] Kenarlardaki sınır sabit hızdadır ve bu da kabuğu batmak.^[53] Altta kullanılan sınır koşulu "Winkler'in esnek tabanı" olarak adlandırılır. Şu anda hidrostatik denge ve tabanın yatay olarak serbestçe kaymasını sağlar.^[53]

Küresel ölçekli

Manto konveksiyonu

Manto konveksiyonunun bir simülasyonu kullanılarak dörtte bir 2D halka şeklinde GÖRÜNÜŞ.^[62][63] Modelde, sıcaklık çekirdek-manto sınırı (iç sınır) 4273 K (yaklaşık 4000 ℃) sabitken, kabuk ve manto arasındaki sınırda (dış sınır) 973 K (yaklaşık 700 ℃).^[62] Simülasyondaki ağ zamanla değişir. Kod kullanır uyarlanabilir ağ iyileştirme Ağ, yükselen dumanlar gibi daha doğru hesaplamaya ihtiyaç duyan alanlarda daha incedir, öte yandan ağ, hesaplama gücünden tasarruf etmek için diğer alanda daha kabadır.^[62] Şekilde, kırmızı renk daha yüksek bir sıcaklığı belirtirken, mavi renk daha soğuk bir sıcaklığı belirtir; sıcak malzeme çekirdek manto sınırı düşük yoğunluk nedeniyle. Sıcak malzeme dış sınıra ulaştığında yatay olarak hareket etmeye başlar ve sonunda soğumadan dolayı batar.

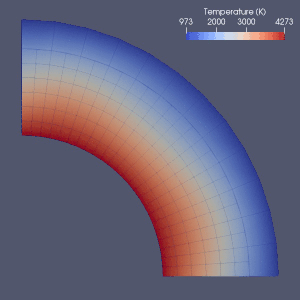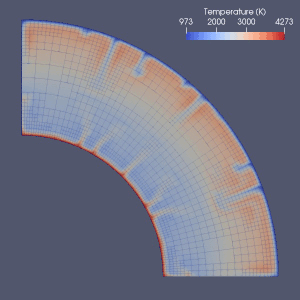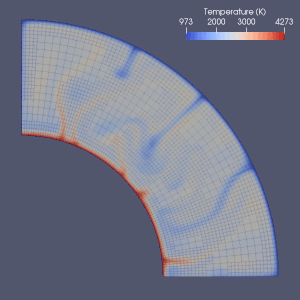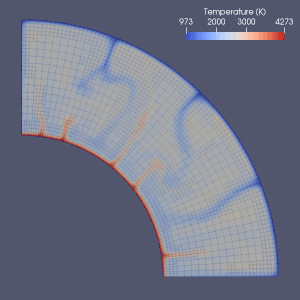
Manto konveksiyonunu modellemek için birçok girişim vardır.

Sonlu elemanlar,^[64] sonlu hacim, Sonlu fark^[65] ve spektral yöntemler hepsi manto konveksiyon modellemesinde kullanıldı ve hemen hemen her model bir Euler ızgarası kullandı.^[2] Sonlu fark ve spektral yöntemlerin basitliği ve hızı nedeniyle, bazı erken modellerde kullanılmış, ancak sonlu eleman veya sonlu hacim yöntemleri genellikle 2010'larda benimsenmiştir.^[2] Pek çok kıyaslama çalışması bu sayısal modellerin geçerliliğini araştırmıştır.^{[2][66][67][68][69][70][71]} Mevcut yaklaşımlar çoğunlukla sabit ve tek tip bir ızgara kullanır.^[2] Daha doğru bir yaklaşım gerektiren kısımda elemanların boyutunun azaltıldığı ızgara iyileştirmesi, muhtemelen manto konveksiyonunun sayısal modellemesinde gelecekteki gelişimin yönüdür.^[2][72]

Sonlu fark yaklaşımı

1960'lardan 1970'lere kadar, sonlu fark yaklaşımını kullanan manto konveksiyon modelleri genellikle ikinci dereceden kullanıldı sonlu farklar.^[2][66] Akış işlevleri basıncın etkisini ortadan kaldırmak ve algoritmanın karmaşıklığını azaltmak için kullanılmıştır.^[2] Bilgisayar teknolojisindeki ilerlemeden dolayı, artık daha doğru bir sonuç elde etmek için daha yüksek dereceli terimlerle sınırlı farklılıklar kullanılmaktadır.^[2][73]

Sonlu hacim yaklaşımı

Sonlu hacim yaklaşımı ile modellenen manto konveksiyonu genellikle basınç ve basınç arasındaki dengeye dayanır. itme. Elde edilen denklemler, her bir elemanın hız ve basınç değerlerinin farklı noktalarda yer aldığı kademeli hız ve basınca sahip bir ızgara kullanan sonlu fark yaklaşımı ile aynıdır.^[2] Bu yaklaşım hız ve basınç arasındaki bağlantıyı sürdürebilir.^[2]

Bu sonlu fark / sonlu hacim yaklaşımına dayalı olarak çoklu kodlar geliştirilir.^{[2][74][75][76][77][65][78]} Dünya'nın üç boyutlu geometrisinin modellenmesinde, mantoların parametreleri farklı ölçeklerde değişiklik gösterdiğinden, multigrid, farklı değişkenler için farklı grid boyutları kullanılması anlamına gelen, zorlukların üstesinden gelmek için uygulanmaktadır.^[2] Örnekler, küp şeklinde küre ızgarasını içerir,^[79][80] 'Yin-Yang' ızgarası,^[81][82][83] ve sarmal ızgara.^[84]

Sonlu eleman yaklaşımı

Sonlu eleman yaklaşımında, akış fonksiyonları denklemlerin karmaşıklığını azaltmak için de sıklıkla kullanılır.^[2] Dolandırıcı,^[85] Mantodaki iki boyutlu sıkıştırılamaz akışı modellemek, 1990'larda manto konveksiyonunu modellemek için kullanılan popüler kodlardan biriydi.^[86][2] Citcom, bir Eulerian mutlgrid sonlu eleman modeli, en popüler programlardan biridir^[2] 2B'de manto konveksiyonunu modellemek için^[87] ve 3D.^[88]

Spektral yöntem

Manto konveksiyonundaki spektral yöntem, üç boyutlu yönetim denklemini birkaç tek boyutlu denkleme böler, bu da denklemleri çok daha hızlı çözer. İlk manto konveksiyon modellerinde popüler yaklaşımlardan biriydi.^[2] 1980'lerden 2000'lerin başına kadar bu yöntem kullanılarak birçok program geliştirildi.^{[2][89][90][91][92][93][94][95]} Bununla birlikte, mantonun viskozitesindeki yanal değişikliklerin bu yaklaşımda yönetilmesi zordur ve diğer yöntemler 2010'larda daha popüler hale gelmiştir.^[2]

Dünya birkaç tabakadan oluşur. Plakaların kinematiğini modellemek için sayısal modeller kullanılabilir.

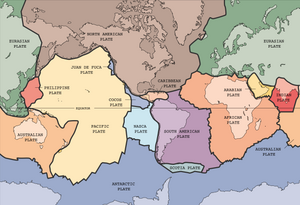
Levha tektoniği

Levha tektoniği Dünya'nın litosfer esas olarak manto üzerinde yüzen plakalardan oluşur.^[96] Manto konveksiyon modeli, üzerinde yüzen plakaların modellenmesinde esastır ve plakaları bu modele dahil etmek için iki ana yaklaşım vardır: rijit blok yaklaşımı ve reolojik yaklaşım.^[2] Rijit blok yaklaşımı plakaların rijit olduğunu varsayar, bu da plakaların şekillerini koruduğu ve su üzerinde yüzen bazı tahta bloklar gibi deforme olmadığı anlamına gelir. Bunun tersine, reolojik yaklaşım plakaları, alttaki litosfere uygulanan denklemlerin üstteki plakalara da uygulandığı yüksek viskoziteli bir sıvı olarak modeller.^[2]

Geodynamo

Doğrulamak için sayısal modeller yapılmıştır. jeodinamo teorisi, jeomanyetik alanın Dünya'nın içindeki iletken demir ve nikel sıvısının hareketi tarafından oluşturulduğunu öne süren bir teori. çekirdek.^[2][97]

Dünyanın sıvı dış çekirdeğinin akışının modellenmesi zordur çünkü:^[2]

• coriolis etkisi Dünya'nın dönüşü nedeniyle göz ardı edilemez
• manyetik alan ayrıca üretecek Lorentz kuvveti sıvı dış çekirdekteki iletken sıvının hareketini etkileyecek olan
• düşük viskozite sıvı Demir sıvı akışının modellenmesini zorlaştırır

Modellerin çoğu, spektral yöntem jeodinamoyu simüle etmek için,^[2][98] örneğin Glatzmaier-Roberts modeli.^[99][100] Modelde sonlu farklar yöntemi de Kageyama ve Sato tarafından kullanılmıştır.^[98][101] Bazı araştırmalar, sonlu hacim gibi diğer yöntemleri de denedi^[102] ve sonlu eleman yöntemleri.^[103]

Akan sıvı dış çekirdek tarafından üretilen manyetik alanı gösteren sayısal bir jeodinamo modeli (Glatzmaier-Roberts modeli).^[104] Bu şekil, Dünya'nın manyetik alanının bir manyetik ters çevirme.

Sismoloji

Dünya boyunca sismik dalga yayılımının simülasyonu.^[1]

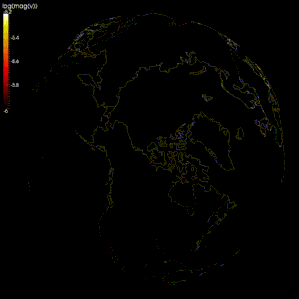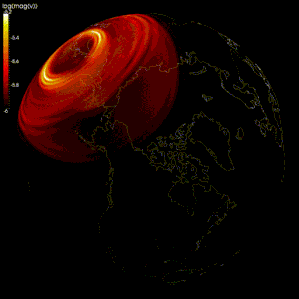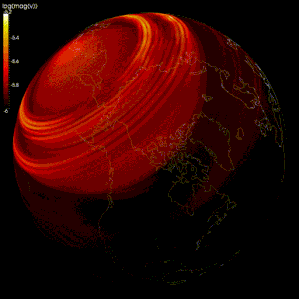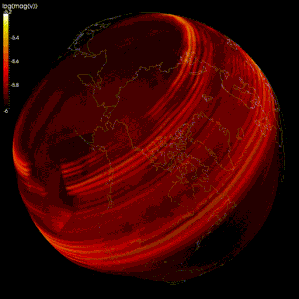
Sonlu fark yöntemleri, yayılma simülasyonlarında yaygın olarak kullanılmıştır. sismik dalgalar.^{[105][106][107]} Bununla birlikte, hesaplama gücündeki sınırlamalar nedeniyle, bazı modellerde, ağın aralığı çok büyüktür (sismik dalgaların dalga boyuna kıyasla), bu nedenle sonuçlar yanlıştır. ızgara dağılımı, farklı frekanslardaki sismik dalgaların ayrıldığı.^[105][108] Bazı araştırmacılar, sismik dalga yayılımını modellemek için spektral yöntemi kullanmayı önermektedir.^[105][109]

Hatalar ve sınırlamalar

Hata kaynakları

Sayısal modelleme jeolojik problemlere doğru nicel tahmin sağlarken, her zaman Aşağıdaki nedenlerden dolayı gerçek gözlem ve modelleme sonuçları arasındaki fark:^[2]

• sayısal modeli oluştururken asıl sorunun basitleştirilmesi.^[2] Bir jeolojik sistemi çok sayıda faktör etkileyebileceğinden, her şeyi hesaba katmak neredeyse imkansızdır. Bu nedenle, sayısal bir model genellikle daha az önemli faktörleri atlayarak gerçek sistemi basitleştirir. Örneğin, Dünya yüzeyindeki dalgalanmaya rağmen, Dünya genellikle bir küre olarak modellenir.
• yönetim denklemlerinin yaklaşımları veya idealleştirmeleri.^[2] Doğadaki birçok nesne karmaşıktır. It is impossible to capture all the characteristics using equations. For instance, rocks are discontinuous, but modeling rock as a continuous material is reasonable at large scale as it describes the properties accurately enough.
• the approximations in the discretization process.^[2] Since the governing equations in the model cannot be solved directly, approximations to these equations are made using discretization and numerical methods.
• the uncertainty in physical parameters.^[2] For example, the models of the viskozite of mantle and core are not accurate.^[110]

Sınırlamalar

Apart from the errors, there are some limitations in using numerical models:

• Users of the models need a high level of knowledge and experience to prevent misuse and misinterpretation of results.^[111]

Ayrıca bakınız

• Jeolojik modelleme
• Sayısal analiz

Referanslar