Zaman ölçeği hesabı - Time-scale calculus

İçinde matematik, zaman ölçeği hesabı teorisinin bir birleşimidir fark denklemleri bununla diferansiyel denklemler, integral ve diferansiyelin birleştirilmesi hesap ile sonlu farklar hesabı, karma ayrık-sürekli çalışmak için bir biçimcilik sunar dinamik sistemler. Kesikli ve sürekli verilerin eşzamanlı modellenmesini gerektiren herhangi bir alanda uygulamaları vardır. Bir türevin yeni bir tanımını verir, öyle ki biri gerçek sayılar üzerinde tanımlanan bir fonksiyonu farklılaştırırsa, o zaman tanım standart farklılaşmaya eşdeğerdir, ancak tamsayılar üzerinde tanımlanan bir fonksiyonu kullanırsa, o zaman bu, ileri fark Şebeke.

Tarih

Zaman ölçeği hesabı 1988'de Alman matematikçi tarafından tanıtıldı Stefan Hilger.^[1] Bununla birlikte, benzer fikirler daha önce kullanılmış ve en azından Riemann – Stieltjes integrali, toplamları ve integralleri birleştiren.

Dinamik denklemler

Diferansiyel denklemlerle ilgili birçok sonuç, fark denklemleri için karşılık gelen sonuçlara oldukça kolay bir şekilde aktarılırken, diğer sonuçlar bunlardan tamamen farklı görünmektedir. sürekli meslektaşları.^[2] Zaman ölçeklerinde dinamik denklemlerin incelenmesi, bu tür tutarsızlıkları ortaya çıkarır ve sonuçların iki kez kanıtlanmasını önlemeye yardımcı olur - biri diferansiyel denklemler için ve bir kez daha fark denklemleri için. Genel fikir, bilinmeyenin alanının olduğu dinamik bir denklem için bir sonuç kanıtlamaktır. işlevi Gerçeklerin keyfi olarak kapalı bir alt kümesi olabilen sözde bir zaman ölçeğidir (bir zaman kümesi olarak da bilinir). Bu şekilde, sonuçlar yalnızca Ayarlamak nın-nin gerçek sayılar veya seti tamsayılar ancak daha genel zaman ölçeklerine Kantor seti.

En popüler üç örnek hesap zaman ölçeklerinde diferansiyel hesap, fark hesabı, ve kuantum hesabı. Zaman ölçeğindeki dinamik denklemler, aşağıdaki gibi uygulamalar için bir potansiyele sahiptir. nüfus dinamikleri. Örneğin, mevsimde sürekli gelişen, kışın yumurtaları inkübasyon halindeyken veya uyku halindeyken ölen böcek popülasyonlarını modelleyebilirler ve ardından yeni bir mevsimde yumurtadan çıkarak örtüşmeyen bir popülasyon oluşturabilirler.

Biçimsel tanımlar

Bir zaman ölçeği (veya ölçü zinciri) bir kapalı alt küme of gerçek çizgi ${ displaystyle mathbb {R}}$. Genel bir zaman ölçeğinin ortak gösterim şekli ${ displaystyle mathbb {T}}$.

Zaman ölçeklerinin en sık karşılaşılan iki örneği gerçek sayılardır. ${ displaystyle mathbb {R}}$ ve ayrık zaman ölçek ${ displaystyle h mathbb {Z}}$.

Zaman ölçeğindeki tek bir nokta şu şekilde tanımlanır:

${ displaystyle t: t in mathbb {T}}$

Zaman ölçeklerinde işlemler

Ayrık bir zaman ölçeğinde ileri atlama, geri atlama ve grenlilik operatörleri

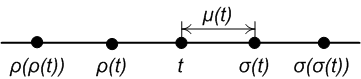
ileri atlama ve geri atlama operatörler, belirli bir noktanın sağında ve solunda zaman ölçeğindeki en yakın noktayı temsil eder ${ displaystyle t}$, sırasıyla. Resmen:

${ displaystyle sigma (t) = inf {s in mathbb {T}: s> t }}$ (ileri kaydırma / atlama operatörü)

${ displaystyle rho (t) = sup {s in mathbb {T}: s$ (geri kaydırma / atlama operatörü)

taneciklilik ${ displaystyle mu}$ bir noktadan sağdaki en yakın noktaya olan mesafedir ve şu şekilde verilir:

${ displaystyle mu (t) = sigma (t) -t.}$

Sağ yoğunluk için ${ displaystyle t}$, ${ displaystyle sigma (t) = t}$ ve ${ displaystyle mu (t) = 0}$.
Sol yoğun ${ displaystyle t}$, ${ displaystyle rho (t) = t.}$

Noktaların sınıflandırılması

Farklı sınıflandırmalara sahip bir zaman ölçeğinde birkaç nokta

Herhangi ${ displaystyle t in mathbb {T}}$, ${ displaystyle t}$ dır-dir:

• sol yoğun Eğer ${ displaystyle rho (t) = t}$
• doğru yoğun Eğer ${ displaystyle sigma (t) = t}$
• dağınık sola Eğer ${ displaystyle rho (t)$
• sağa dağılmış Eğer ${ displaystyle sigma (t)> t}$
• yoğun hem sol yoğun hem de sağ yoğunsa
• yalıtılmış hem sola dağılmış hem de sağa dağılmışsa

Sağdaki şekilde gösterildiği gibi:

• Nokta ${ displaystyle t_ {1}}$ dır-dir yoğun
• Nokta ${ displaystyle t_ {2}}$ dır-dir sol yoğun ve sağa dağılmış
• Nokta ${ displaystyle t_ {3}}$ dır-dir yalıtılmış
• Nokta ${ displaystyle t_ {4}}$ dır-dir dağınık sola ve doğru yoğun

Süreklilik

Süreklilik Bir zaman ölçeğinin yoğunluğu yeniden tanımlanır. Bir zaman ölçeğinin olduğu söyleniyor noktada sağ sürekli ${ displaystyle t}$ noktada doğru yoğunsa ${ displaystyle t}$. Benzer şekilde, bir zaman ölçeğinin noktada sürekli sol ${ displaystyle t}$ noktada yoğun bırakılırsa ${ displaystyle t}$.

Türev

Bir işlev al:

${ displaystyle f: mathbb {T} rightarrow mathbb {R}}$,

(nerede olabilir) Banach alanı, ancak basitlik için gerçek satıra ayarlanmıştır).

Tanım: The delta türevi (ayrıca Hilger türevi) ${ displaystyle f ^ { Delta} (t)}$ ancak ve ancak aşağıdaki durumlarda mevcuttur:

Her biri için ${ displaystyle epsilon> 0}$ bir mahalle var ${ displaystyle U}$ nın-nin ${ displaystyle t}$ öyle ki:

${ displaystyle | f ( sigma (t)) - f (s) -f ^ { Delta} (t) ( sigma (t) -s) | leq varepsilon | sigma (t) -s | }$

hepsi için ${ displaystyle s}$ içinde ${ displaystyle U}$.

Al ${ displaystyle mathbb {T} = mathbb {R}.}$ Sonra ${ displaystyle sigma (t) = t}$, ${ displaystyle mu (t) = 0}$, ${ displaystyle f ^ { Delta} = f '}$; standartta kullanılan türevdir hesap. Eğer ${ displaystyle mathbb {T} = mathbb {Z}}$ ( tamsayılar ), ${ displaystyle sigma (t) = t + 1}$, ${ displaystyle mu (t) = 1}$, ${ displaystyle f ^ { Delta} = Delta f}$ ... ileri fark operatörü fark denklemlerinde kullanılır.

Entegrasyon

delta integrali delta türevine göre ters türev olarak tanımlanır. Eğer ${ displaystyle F (t)}$ sürekli bir türevi vardır ${ displaystyle f (t) = F ^ { Delta} (t)}$ bir set

${ displaystyle int _ {r} ^ {s} f (t) Delta (t) = F (s) -F (r).}$

Laplace dönüşümü ve z dönüşümü

Bir Laplace dönüşümü herhangi bir rasgele zaman ölçeği için aynı dönüşüm tablosunu kullanan zaman ölçeklerindeki işlevler için tanımlanabilir. Bu dönüşüm, zaman ölçeklerinde dinamik denklemleri çözmek için kullanılabilir. Zaman ölçeği negatif olmayan tamsayılarsa, dönüşüm eşittir^[2] değiştirilmiş Z-dönüşümü:

${ displaystyle { mathcal {Z}} ' {x [z] } = { frac {{ mathcal {Z}} {x [z + 1] }} {z + 1}}}$

Kısmi farklılaşma

Kısmi diferansiyel denklemler ve kısmi fark denklemleri zaman ölçeklerinde kısmi dinamik denklemler olarak birleştirilir.^[3][4][5]

Çoklu entegrasyon

Çoklu entegrasyon zaman ölçeklerinde Bohner (2005) 'de ele alınmıştır.^[6]

Zaman ölçeklerinde stokastik dinamik denklemler

Stokastik diferansiyel denklemler ve stokastik fark denklemleri, zaman ölçeklerinde stokastik dinamik denklemlere genellenebilir.^[7]

Teoriyi zaman ölçeklerinde ölçün

Her zaman ölçeği ile ilişkili doğal bir ölçü^[8][9] ile tanımlanmış

${ displaystyle mu ^ { Delta} (A) = lambda ( rho ^ {- 1} (A)),}$

nerede ${ displaystyle lambda}$ gösterir Lebesgue ölçümü ve ${ displaystyle rho}$ geriye doğru kaydırma operatörü ${ displaystyle mathbb {R}}$. Delta entegrali olağan hale gelir Lebesgue – Stieltjes integrali bu önlemle ilgili olarak

${ displaystyle int _ {r} ^ {s} f (t) Delta t = int _ {[r, s)} f (t) d mu ^ { Delta} (t)}$

ve delta türevi ortaya çıkıyor Radon-Nikodym türevi bu önlemle ilgili olarak^[10]

${ displaystyle f ^ { Delta} (t) = { frac {df} {d mu ^ { Delta}}} (t).}$

Zaman ölçeklerinde dağılımlar

Dirac delta ve Kronecker deltası zaman ölçeklerinde birleştirilmiştir. Hilger deltası:^[11][12]

${ displaystyle delta _ {a} ^ { mathbb {H}} (t) = { begin {case} { frac {1} { mu (a)}}, & t = a 0, & t neq a end {vakalar}}}$

Zaman ölçeklerinde integral denklemler

İntegral denklemler ve toplama denklemleri zaman ölçeklerinde integral denklemler olarak birleştirilir.^{[kaynak belirtilmeli ]}

Zaman ölçeklerinde kesirli hesap

Kesirli hesap zaman ölçeklerinde Bastos, Mozyrska ve Torres'te ele alınır.^[13]

Ayrıca bakınız

• Fraktal analizi bir üzerindeki dinamik denklemler için Kantor seti.

Referanslar

daha fazla okuma

• Agarvval, Ravi; Bohner, Martin; O’Regan, Donal; Peterson, Allan (2002). "Zaman ölçeklerinde dinamik denklemler: bir anket". Hesaplamalı ve Uygulamalı Matematik Dergisi. 141 (1–2): 1–26. Bibcode:2002JCoAM.141 .... 1A. doi:10.1016 / S0377-0427 (01) 00432-0.
• Zaman Ölçeklerinde Dinamik Denklemler Özel sayısı Hesaplamalı ve Uygulamalı Matematik Dergisi (2002)
• Dinamik Denklemler ve Uygulamalar Özel Sayısı Fark Denklemlerindeki Gelişmeler (2006)
• Zaman Ölçeklerinde Dinamik Denklemler: Nitel Analiz ve Uygulamalar Özel sayısı Doğrusal Olmayan Dinamik ve Sistem Teorisi (2009)

Dış bağlantılar

• Baylor Üniversitesi Zaman Ölçekleri Grubu
• Timescalewiki.org